Excel - Bilinear interpolation function (UDF)

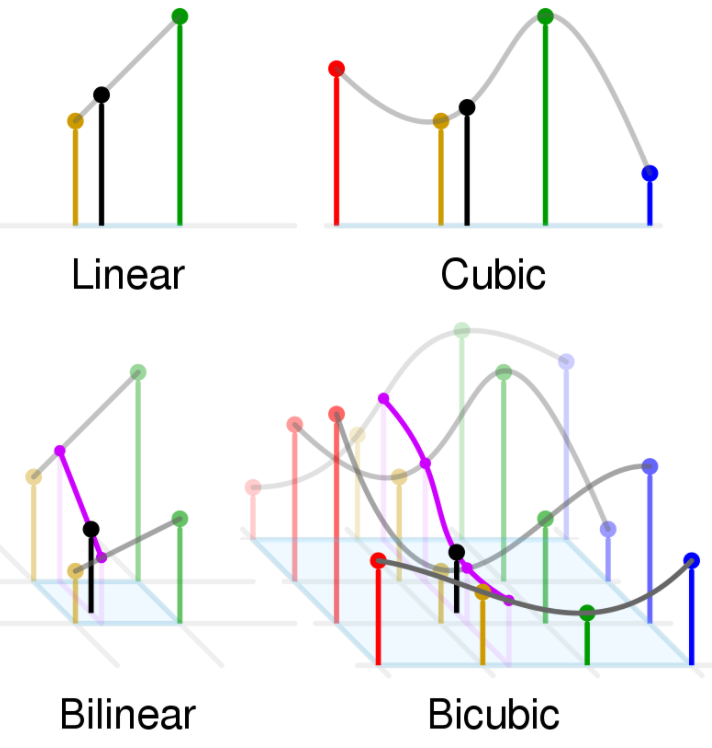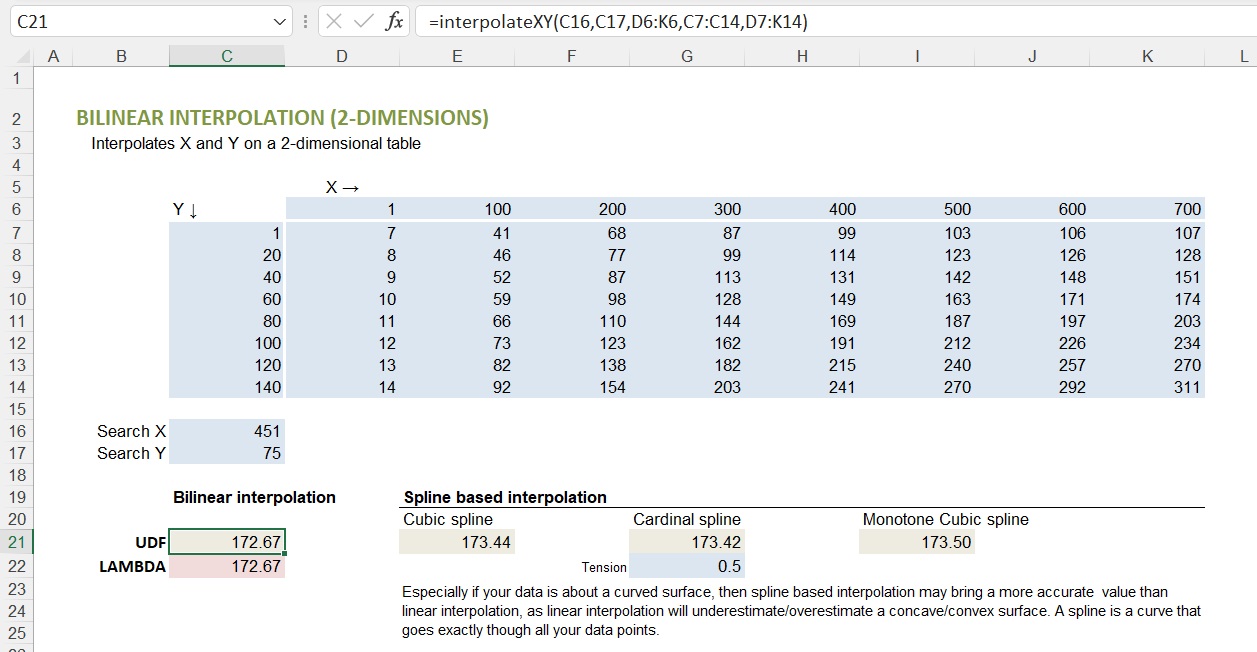
Calculation explanation of above example - Bilinear interpolation

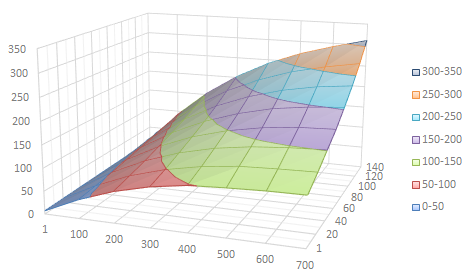
Visualisation of the data table above

Calculation
X = 451 lies between X = 400 and X = 500. X-fraction = (451 - 400)/(500 - 400) = 0.51
Y = 75 lies between Y = 60 and Y = 80. Y-fraction = (75 - 60)/(80 - 60) = 0.75

The 4 data point values to interpolate between are (X,Y):
     1. (400,60) = 149
     2. (500,60) = 163
     3. (400,80) = 169
     4. (500,80) = 187

Interpolation X:
     1.&2. → 149 + 0.51 × (163 - 149) = 156.14
     3.&4. → 169 + 0.51 × (187 - 169) = 178.18

Interpolation Y:
     156.14 + 0.75 × (178.18 - 156.14) = 172.67 = final bilineair interpolation result.

The Cubic spline based interpolation brings 173.44, which is 0.4% higher. If your data is about a concave curved surface, it is obvious that the bilinear interpolation result will always slightly underestimate, except on a data point itself. The above example is slightly convex in Y direction, but more dominantly concave in X direction.

Bilinear interpolation - VBA code to be put in a module

In MS Excel, press Alt+F11 to open the Visual Basic Editor (Windows). Via top menu: Insert → Module. Copy the code below into the module.

Public Function InterpolateXY(ByRef X As Range, ByRef Y As Range, ByRef XRange As Range, ByRef YRange As Range, ByRef ValueTable As Range) As Double
    
    'if X or Y fall outside the table, the function result is an error value
    If (X < WorksheetFunction.Min(XRange)) Or (X > WorksheetFunction.Max(XRange)) Or (Y < WorksheetFunction.Min(YRange)) Or (Y > WorksheetFunction.Max(YRange)) Then
        InterpolateXY = CVErr(xlErrNA)
        Exit Function
    End If
    
    Dim X1, X2, Y1, Y2, PX1, PX2, PY1, PY2, V1, V2, V3, V4, FX, FY, C12, C34
    
    'Determine data table points around searchvalues
    X1 = WorksheetFunction.XLookup(X, XRange, XRange, , -1)
    X2 = WorksheetFunction.XLookup(X, XRange, XRange, , 1)
    Y1 = WorksheetFunction.XLookup(Y, YRange, YRange, , -1)
    Y2 = WorksheetFunction.XLookup(Y, YRange, YRange, , 1)
    
    PX1 = WorksheetFunction.Match(X1, XRange, 0)
    PX2 = WorksheetFunction.Match(X2, XRange, 0)
    PY1 = WorksheetFunction.Match(Y1, YRange, 0)
    PY2 = WorksheetFunction.Match(Y2, YRange, 0)
    
    V1 = ValueTable(PY1, PX1)
    V2 = ValueTable(PY1, PX2)
    V3 = ValueTable(PY2, PX1)
    V4 = ValueTable(PY2, PX2)
    
    'X and Y fractions
    If (X2 = X1) Then FX = 0 Else FX = (X - X1) / (X2 - X1)
    If (Y2 = Y1) Then FY = 0 Else FY = (Y - Y1) / (Y2 - Y1)

'2 intermediate results after interpolation on X
    C12 = V1 + FX * (V2 - V1)
    C34 = V3 + FX * (V4 - V3)
    
    'final result after interpolation on Y
    InterpolateXY = C12 + FY * (C34 - C12)
    
End Function

LAMBDA function L_InterpolateXY

Based on L_InterpolateX, so you need to copy in both functions.

LAMBDA function L_InterpolateX

Non-linear, spline based interpolation - Main functions and sub functions VBA code

Public Function interpolateXY_CubicSpline(ByRef x As Range, ByRef y As Range, ByRef XRange As Range, ByRef YRange As Range, ByRef ValueTable As Range) As Double
    
    'if X or Y fall outside the table, the function result is an error value
    If (x < WorksheetFunction.Min(XRange)) Or (x > WorksheetFunction.Max(XRange)) Or (y < WorksheetFunction.Min(YRange)) Or (y > WorksheetFunction.Max(YRange)) Then
        interpolateXY_CubicSpline = CVErr(xlErrNA)
        Exit Function
    End If
    
    Dim X1, X2, Y1, Y2, PX1, PX2, PY1, PY2, V1, V2, V3, V4, FX, FY, C12, C34
    Dim i As Long
    
    i = YRange.Count
    Dim arr() As Double
    ReDim arr(i)
    For i = 0 To YRange.Count - 1
        'transpose as assumption is input in regular table format
        arr(i) = CubicSpline_SP(WorksheetFunction.Transpose(XRange), WorksheetFunction.Transpose(ValueTable.Rows(i + 1)), x)
    Next
    
    interpolateXY_CubicSpline = CubicSpline_SP(YRange, WorksheetFunction.Transpose(arr), y)
    
End Function

Public Function interpolateXY_CardinalSpline(ByRef x As Range, ByRef y As Range, ByRef XRange As Range, ByRef YRange As Range, ByRef ValueTable As Range, tension As Single) As Double
    
    'if X or Y fall outside the table, the function result is an error value
    If (x < WorksheetFunction.Min(XRange)) Or (x > WorksheetFunction.Max(XRange)) Or (y < WorksheetFunction.Min(YRange)) Or (y > WorksheetFunction.Max(YRange)) Then
        interpolateXY_CardinalSpline = CVErr(xlErrNA)
        Exit Function
    End If
    
    Dim X1, X2, Y1, Y2, PX1, PX2, PY1, PY2, V1, V2, V3, V4, FX, FY, C12, C34
    Dim i As Long
    
    i = YRange.Count
    Dim arr() As Double
    ReDim arr(i)
    For i = 0 To YRange.Count - 1
        'transpose as assumption is input in regular table format
        arr(i) = CardinalSpline_SP(WorksheetFunction.Transpose(XRange), WorksheetFunction.Transpose(ValueTable.Rows(i + 1)), tension, x)
    Next
    
    interpolateXY_CardinalSpline = CardinalSpline_SP(YRange, WorksheetFunction.Transpose(arr), tension, y)
    
End Function

Public Function interpolateXY_MonotoneCubicSpline(ByRef x As Range, ByRef y As Range, ByRef XRange As Range, ByRef YRange As Range, ByRef ValueTable As Range) As Double
    
    'if X or Y fall outside the table, the function result is an error value
    If (x < WorksheetFunction.Min(XRange)) Or (x > WorksheetFunction.Max(XRange)) Or (y < WorksheetFunction.Min(YRange)) Or (y > WorksheetFunction.Max(YRange)) Then
        interpolateXY_MonotoneCubicSpline = CVErr(xlErrNA)
        Exit Function
    End If
    
    Dim X1, X2, Y1, Y2, PX1, PX2, PY1, PY2, V1, V2, V3, V4, FX, FY, C12, C34
    Dim i As Long
    
    i = YRange.Count
    Dim arr() As Double
    ReDim arr(i)
    For i = 0 To YRange.Count - 1
        'transpose as assumption is input in regular table format
        arr(i) = MonotoneCubicSpline_SP(WorksheetFunction.Transpose(XRange), WorksheetFunction.Transpose(ValueTable.Rows(i + 1)), x)
    Next
    
    interpolateXY_MonotoneCubicSpline = MonotoneCubicSpline_SP(YRange, WorksheetFunction.Transpose(arr), y)
    
End Function

Public Function CubicSpline_SP(DatapointsX, DatapointsY, ByVal atX As Single) As Double
    Dim n, i As Long
    Dim xin, yin As Variant
    Dim p, sig, h, b, a, k As Double
    Dim klo, khi As Long
    Dim X1, X2
    
    'trick: transpose to get rid of second dimension of range - with input data sitting in a regular table with records in rows
    xin = Application.Transpose(DatapointsX)
    yin = Application.Transpose(DatapointsY)
    
    n = UBound(xin)
    
    ReDim u(n - 1) As Single
    ReDim yt(n) As Single
    yt(1) = 0
    u(1) = 0
    For i = 2 To n - 1
        sig = (xin(i) - xin(i - 1)) / (xin(i + 1) - xin(i - 1))
        p = sig * yt(i - 1) + 2
        yt(i) = (sig - 1) / p
        u(i) = (yin(i + 1) - yin(i)) / (xin(i + 1) - xin(i)) - (yin(i) - yin(i - 1)) / (xin(i) - xin(i - 1))
        u(i) = (6 * u(i) / (xin(i + 1) - xin(i - 1)) - sig * u(i - 1)) / p
    Next i
    yt(n) = 0
    For i = n - 1 To 1 Step -1
        yt(i) = yt(i) * yt(i + 1) + u(i)
    Next i
    
    X1 = WorksheetFunction.XLookup(atX, xin, xin, , -1)
    X2 = WorksheetFunction.XLookup(atX, xin, xin, , 1)
    klo = WorksheetFunction.Match(X1, xin, 0)
    khi = WorksheetFunction.Match(X2, xin, 0)
    
    If (klo = khi) Then
        CubicSpline_SP = yin(klo)
    Else
        h = xin(khi) - xin(klo)
        a = (xin(khi) - atX) / h
        b = (atX - xin(klo)) / h
        CubicSpline_SP = a * yin(klo) + b * yin(khi) + ((a ^ 3 - a) * yt(klo) + (b ^ 3 - b) * yt(khi)) * (h ^ 2) / 6
    End If
End Function

Public Function CardinalSpline_SP(DatapointsX, DatapointsY, ByVal tension As Single, atX)

Dim xin As Variant, yin As Variant
    Dim ptsX()
    Dim ptsY()
    Dim iRow, i, op, r As Long
    Dim n As Integer
    Dim t, thi, tlo, x, xnow, y As Double
    Dim klo, khi As Long
    Dim X1, X2
    
     'trick: transpose to get rid of second dimension of range
    xin = Application.Transpose(DatapointsX)
    yin = Application.Transpose(DatapointsY)
    n = UBound(xin)
	
	'sort in ascending X order
    Dim tmp
    If xin(1) > xin(n) Then
        'swap values
        For i = 1 To WorksheetFunction.RoundDown(n / 2, 0)
            tmp = xin(i)
            xin(i) = xin(n + 1 - i)
            xin(n + 1 - i) = tmp
            tmp = yin(i)
            yin(i) = yin(n + 1 - i)
            yin(n + 1 - i) = tmp
        Next
    End If
	
    ReDim ptsX(n + 2)
    ReDim ptsY(n + 2)
    For i = 1 To n
        ptsX(i) = xin(i)
        ptsY(i) = yin(i)
    Next
    ptsX(0) = ptsX(1)
    ptsX(n + 1) = ptsX(n)
    ptsX(n + 2) = ptsX(n)
    ptsY(0) = ptsY(1)
    ptsY(n + 1) = ptsY(n)
    ptsY(n + 2) = ptsY(n)
    
    'spline calculation
    For i = 0 To n + 2
        If ptsX(i) > atX Then Exit For
    Next
    i = i - 1
    
    If atX = ptsX(i) Then
        CardinalSpline_SP = ptsY(i)
    Else
        thi = 1
        tlo = 0
        r = 0
        Do
            r = r + 1
            t = (thi + tlo) / 2
            x = tension * (-t ^ 3 + 2 * t ^ 2 - t) * ptsX(i - 1) + _
                tension * (-t ^ 3 + t ^ 2) * ptsX(i) + _
                          (2 * t ^ 3 - 3 * t ^ 2 + 1) * ptsX(i) + _
                tension * (t ^ 3 - 2 * t ^ 2 + t) * ptsX(i + 1) + _
                         (-2 * t ^ 3 + 3 * t ^ 2) * ptsX(i + 1) + _
                tension * (t ^ 3 - t ^ 2) * ptsX(i + 2)
            If atX > x Then tlo = t Else thi = t
        Loop Until (Abs(x - atX) < 0.00001) Or (r > 10000)
        y = tension * (-t ^ 3 + 2 * t ^ 2 - t) * ptsY(i - 1) + _
            tension * (-t ^ 3 + t ^ 2) * ptsY(i) + _
                      (2 * t ^ 3 - 3 * t ^ 2 + 1) * ptsY(i) + _
            tension * (t ^ 3 - 2 * t ^ 2 + t) * ptsY(i + 1) + _
                     (-2 * t ^ 3 + 3 * t ^ 2) * ptsY(i + 1) + _
            tension * (t ^ 3 - t ^ 2) * ptsY(i + 2)
        CardinalSpline_SP = y
    End If
End Function

Public Function MonotoneCubicSpline_SP(DatapointsX, DatapointsY, ByVal atX)
    
    Dim n As Long, i As Long, iRow, op, s As Long
    Dim xin As Variant, yin As Variant
    Dim m, mNext, dx, dxNext, common, c1, m_, invDx, common_, h, diff
    Dim c1s()
    Dim klo, khi As Long
    Dim X1, X2
    
    'trick: transpose to get rid of second dimension of range
    xin = Application.Transpose(DatapointsX)
    yin = Application.Transpose(DatapointsY)
    n = UBound(xin)
    
    'Get consecutive differences and slopes
    ReDim dxs(n)
    ReDim dys(n)
    ReDim ms(n)
    
    For i = 1 To n - 1
        dxs(i) = xin(i + 1) - xin(i)
        dys(i) = yin(i + 1) - yin(i)
        ms(i) = dys(i) / dxs(i)
    Next i
    
    'Get degree-1 coefficients
    ReDim c1s(1 To n + 1)
    c1s(1) = ms(1)
    For i = 1 To n - 1
        m = ms(i)
        mNext = ms(i + 1)
        If (m * mNext <= 0) Then
            c1s(i + 1) = 0
        Else
            dx = dxs(i)
            dxNext = dxs(i + 1)
            common = dx + dxNext
            c1s(i + 1) = 3 * common / ((common + dxNext) / m + (common + dx) / mNext)
        End If
    Next
    c1s(n) = ms(n - 1)
    
    'Get degree-2 and degree-3 coefficients
    ReDim c2s(n)
    ReDim c3s(n)
    For i = 1 To n - 1
        c1 = c1s(i)
        m_ = ms(i)
        invDx = 1 / dxs(i)
        common_ = c1 + c1s(i + 1) - m_ - m_
        c2s(i) = (m_ - c1 - common_) * invDx
        c3s(i) = common_ * invDx * invDx
    Next
    
    X1 = WorksheetFunction.XLookup(atX, xin, xin, , -1)
    X2 = WorksheetFunction.XLookup(atX, xin, xin, , 1)
    klo = WorksheetFunction.Match(X1, xin, 0)
    khi = WorksheetFunction.Match(X2, xin, 0)
    
    If (klo = khi) Then
        MonotoneCubicSpline_SP = yin(klo)
    Else
        If klo > khi Then 'X-axis values were in descending order
            Dim tmp
            tmp = klo
            klo = khi
            khi = tmp
        End If
        diff = (atX - xin(klo))
        MonotoneCubicSpline_SP = yin(klo) + c1s(klo) * diff + c2s(klo) * diff * diff + c3s(klo) * diff * diff * diff
    End If
End Function

Excel - Bilinear interpolation function & spline based 2-dimensional interpolation functions

Calculation explanation of above example - Bilinear interpolation

Bilinear interpolation - VBA code to be put in a module

LAMBDA function L_InterpolateXY

LAMBDA function L_InterpolateX

Non-linear, spline based interpolation - Main functions and sub functions VBA code

Excel - Bilinear interpolation function &
spline based 2-dimensional interpolation functions